حذف نویز واصلاح تصویر در متلب
ادامه آموزش نرم افزار متلب بخش 19
در این مبحث آشنا میشویم با :
1- فرمول پایه اصلاح تصویر
2- نویز متناوب با فرکانس معلوم
3- آشنایی با انواع فیلترهای مکانی
4- پیاده سازی فیلترها
یکی از کاربرد های بحث پردازش تصویربحث اصلاح و باز یافت تصاویر و حذف نویز است .
همه روش هایی که میپردازند به بخش اصلاح تصویراز یک فرمول پایه استفاده میکنند .
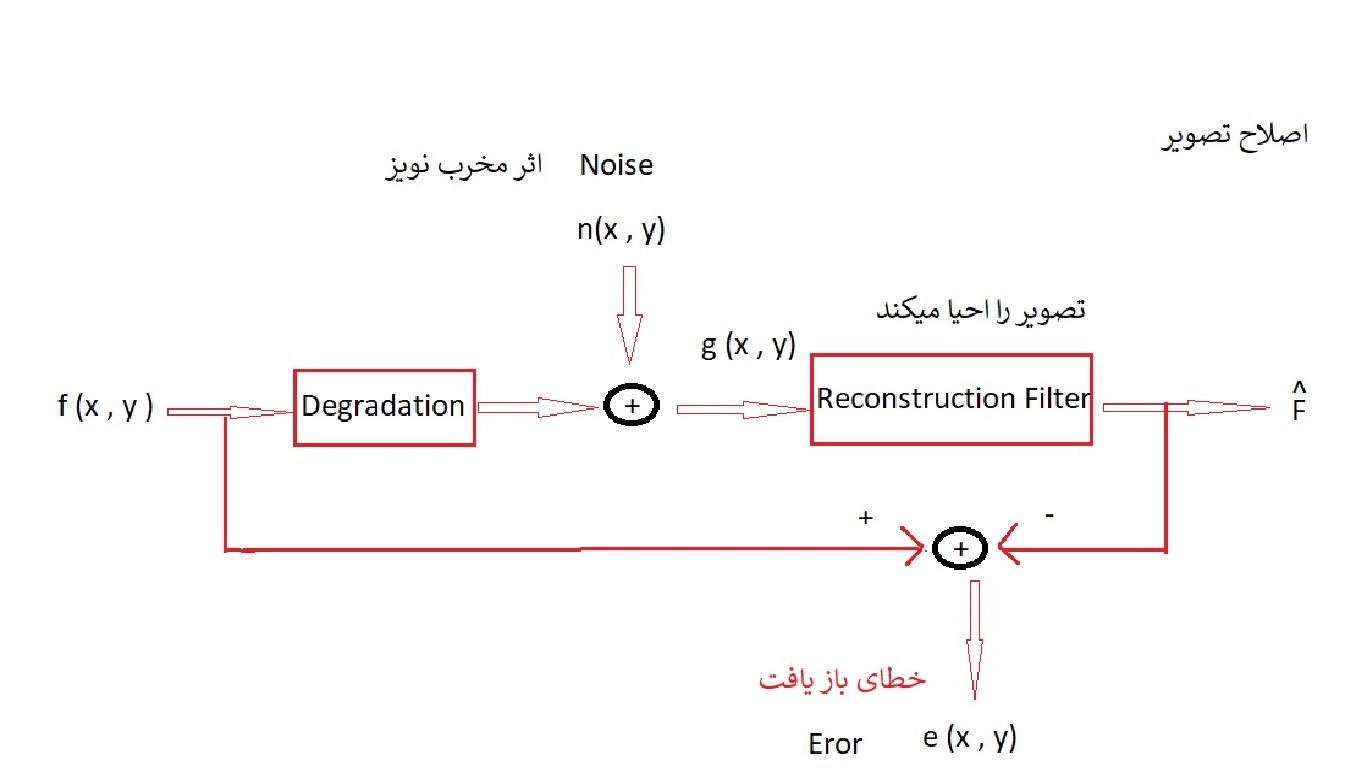
هدف پیدا کردن روش هایی است که بتوانیم از g برسیم به (اِف هَد) f^ که تقریبی از تصویر اصلی است .

در حالت کلی N , H را نداریم و پیدا کردن مدل دقیق خطا غیر ممکن است مگر حالت خاصی باشد مثلا دقیقا بدانیم خطا چه بود یا مدل نویز را بدانیم
نویز متناوب با فرکانس معلوم یکی از ساده ترین حالت ها است .
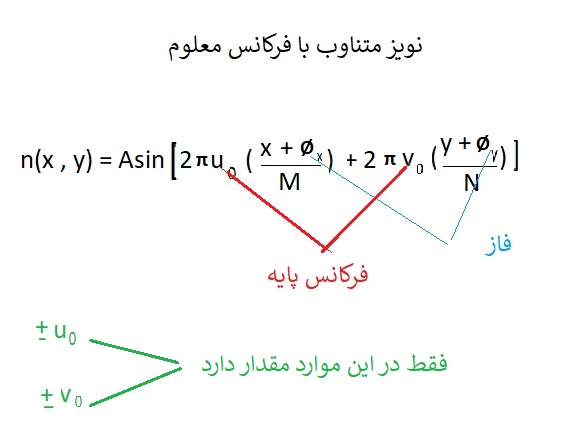
تابع دلتای دیراک که متمرکز است روی چهارترکیب ( +u , – u , -v , +v )
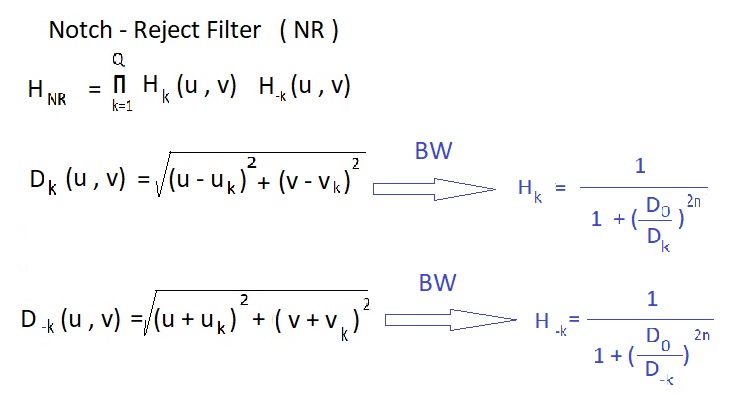
تا زمانی که u به uk نزدیک است صفر میشود وقتی که در بینهایت است یک میشود ، یعنی هر چیزی که نزدیک فرکانس uk است حذف میکند .
انواع فیلتر های مکانی برای حذف نویز :
-
میانگین یا Average در محیط متلب با تابع fspecial با سوییچ average پیاده سازی میشود .
-
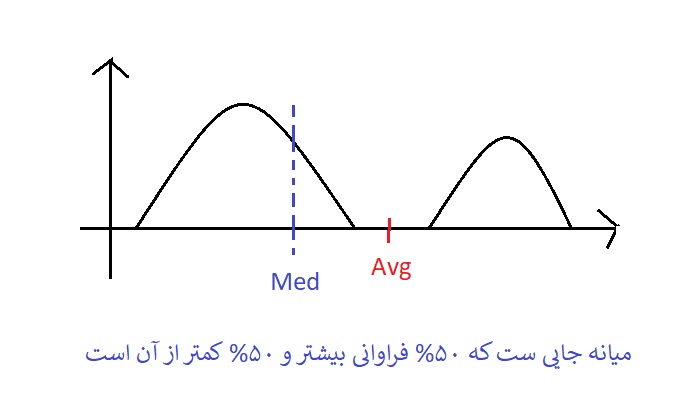
میانه یا Medianدر محیط متلب با تابع medfilt2 پیاده سازی میشود ،یک مزیتی که میانه دارد این است که همیشه داده ای را میدهد که بین داده های ورودی هست .
-
میانگین هندسی در محیط متلب با تابع colfilt پیاده سازی میشود .
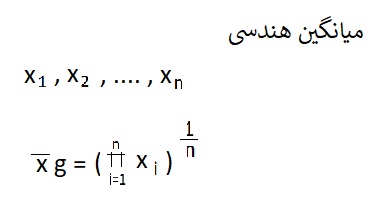
-
میانگین توافقی یا هارمونیک در محیط متلب با تابع colfilt پیاده سازی میشود .

-
شبه هارمونیک یا Contra harmonicدر محیط متلب با تابع colfilt پیاده سازی میشود .
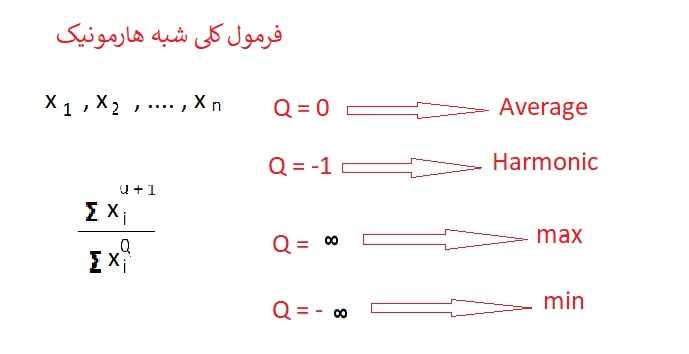
-
فیلتر بیشینه Max در محیط متلب با تابع ordfilt2 پیاده سازی میشود .
-
فیلتر کمینه Min در محیط متلب با تابع ordfilt2 پیاده سازی میشود.
-
نقطه میانی mid-point در محیط متلب با تابع colfilt پیاده سازی میشود .

-
بریدن یا حذف کردن از ابتدا یا انتها Alpha – trim
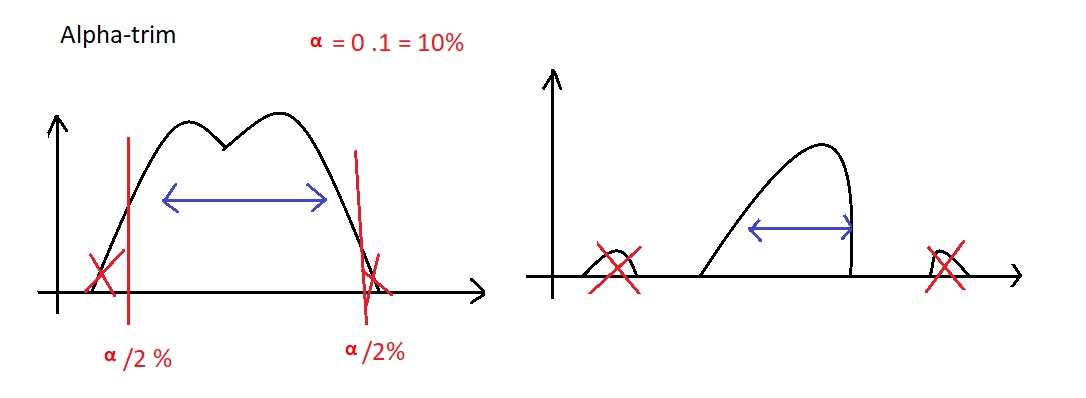
با هر کدام از این فیلتر ها میتوانیم نویزهایی خاص را از تصویرحذف کنیم .
از این فیلترها برای پلاک خوانی در نرم افزار پارکینگ و اتوماسیون پارکینگ استفاده میگردد. از اتوماسیون پارکینگ در نرم افزار کنترل تردد خودرو استفاده میگردد.
پیاده سازی فیلترها :
function g = spatialFilter ( Type , Size , Varargin )
if nargin < 3 I I isempty ( size )
size = [3 3] ;
end
if nume 1 (size ) = = 1
size = [size size] ;
end
Type = Lower ( Type ) ;
Switch Type
Case ‘ median ‘
g = medfilt2 ( f , size ) ;
Case { ‘ average ‘ , ‘ mean ‘ }
W = fspecial ( ‘average ‘ , size ) ;
G = imfilter ( f , w ) ;
Case { ‘ geomtric ‘ , ‘gmean’ , ‘geomean’ , ‘ geomtricmean ‘}
g = colfilt (f , size , ‘ sliding ‘ , @GeomtricMean ) ;
Case { ‘ harmonic ‘ , ‘ hmean ‘ , ‘ harmean ‘ , ‘ harmonicmean ‘}
g = colfilt (f , size , ‘ sliding ‘ , @ HarmonicMean) ;
Case { ‘ charmonic ‘ , ‘ contraharmonic ‘}
if isempty ( Varargin )
Q = 1 ;
else
Q = Varargin } 1 { ;
end
fun = @ (X) ContraHarmonicMean ( X , Q ) ;
g = colfilt (f , size , ‘ sliding ‘ , fun ) ;
Case ‘ max ‘
g= ordfilt2 (f , prod ( size) , true ( size ) ) ;
Case ‘ min ‘
g= ordfilt2 ( f , 1 , true ( size ) ) ;
Case ‘ midpoint ‘
gmin = ordfilt2 ( f , 1 , true ( size ) ) ;
gmax= ordfilt2 (f , prod ( size) , true ( size ) ) ;
g=( gmin + gmax ) /2 ;
Case ‘ alphatrim ‘
if isempty ( Varargin )
alpha = 0 . 1 ;
else
alpha = Varargin } 1 { ;
end
fun = @ ( X ) AlphaTrimMean ( x , alpha ) ;
g = colfilt ( f , size , ‘ sliding ‘ , fun ) ;
Other wise
Error ( ‘ Undefined filter type . ‘ ) ;
end
function gm= GeomtricMean (X)
gm= exp (mean (Log ( X ) ) ) ;
end
function hm = HarmonicMean (X)
hm= 1./mean (1./X) ;
end
function chm= ContraHarmonicMean (X)
Chm= Sum ( X . ^ (Q+1) ) ./Sum( X . ^ Q ) ;
end
function atm = AlphaTrimMean ( X , alpha )
atm = zeros ( 1 , size ( x , 2 ) ) ;
for j = 1 : nume 1 (atm )
xtj = AlphaTrim ( x ( : , j ) , alpha ) ;
atm ( j ) = mean ( xtj ) ;
end
function xt= AlphaTrim ( X , alpha )
nx = numel ( X ) ;
nt = 2*round ( alpha * nx/2 ) ;
xt = sort ( X ) ;
xt ( [ 1 : nt/2 end – nt/2 + 1 : end ] ) = [ ] ;
end



