حذف نویز واصلاح تصویر در متلب 3 (21)

حذف نویز واصلاح تصویر در متلب 3

روش آماری NSPR در نرم افزار متلب

ادامه آموزش نرم افزار متلب بخش 21

در این مبحث آشنا میشویم با :

1- روش آماری NSPR

2- تخمین با روش آماری واریانس

3- فراخوانی به روش J = deconvwnr ( I , PSF , NSR )

4- فرا خوانی به روش J = deconvwnr ( I , PSF , NCORR , ICORR )

در روش آماری NSPR در متلب وقتی خط بالای NSPR را نمینویسیم منظور این است که NSPR ثابت است .

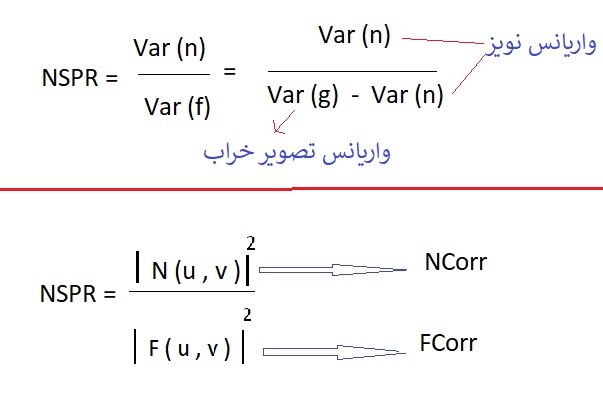
فرمول روش آماری NSPR در متلب

این روش از دید آماری NSPR را توصیف میکند همان مفهوم قبل را دارد .

PSFهمان ماتریس وزنی که برای تبدیل مکانی استفاده میشود .

NSRاندازه نویز به سیگنال را نشان میدهد که یک پارامتر است .

NCORR کُریلیشن نویز با خودش .

ICORR کُریلیشن تصویر با خودش .

ببینیم برای حذف نویز تا چه حد مورد استفاده قرار میگیرد .

Clc ;
Clear ;
Close all ;
% % Read Image
f =imread ( ‘ Cameraman . tif ‘ ) ;
f = im2double (f) ;
% % Apply Motion Filter
MotionLength = 7 ;
MotionAngle = 45 ;
PSF = fspecial ( ‘ motion ‘ , MotionLength , MotionAngle ) ;
g1 = imfilter ( f , PSF) ;
% % Add Noise
NoiseMean = 0 ;
NoiseVar = 0 . 01 ;
g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
% % Wiener Deconvolution

% % Results
figure ;
subplot ( 2 , 2 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 2 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 2 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;

نمونه تصویر نویزی متلب

تصویری که 45 درجه چرخش داشته و نویز دارشده را میخواهیم با استفاده از دستور J = deconvwnr ( I , PSF , NSR ) باز یابی کنیم :

با فرض این که PSF را داریم .

با روش آماری واریانس تخمین میزنیم .

% % Wiener Deconvolution
% ImageVar = Var (f(:)) ;
% NSPR = NoiseVar ;
Fhat 1 = deconvwnr (g2 , PSF , 0 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;

روش آماری NSPR در متلب

با این فرض که هیچ نویزی وجود ندارد چنین تصویری میدهد که نتیجه رضایت بخشی برای ما نیست .

از پردازش تصویر در نرم افزار پلاک خوان و اتوماسیون پارکینگ و نیز نرم افزار پارکینگ استفاده میگردد.

حالا بیایم و با استفاده از تحلیل آماری NSPR را پیدا کنیم .

% % Add Noise
NoiseMean = 0 ;
NoiseVar = 0 . 001 ;
g2 = imnoise ( g1 , ‘gaussian ‘ , NoiseMean , NoiseVar ) ;
% % Wiener Deconvolution
NSPR1 = 0 ;
Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
ImageVar = Var (f (:) ) ;
NSPR2 = NoiseVar / ImageVar ;
Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
subplot ( 2 , 3 , 5) ;
imshow ( fhat2 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘  ] ) ;

روش آماری NSPR در متلب

واریانس نویز را هم ده برابرکمتر کردیم توانست اثر حرکت را حذف کند فقط اثر نویز حذف نشده که با یک روش دیگری این را بهبود میدهیم . از نظر وضوح نزدیکتر به تصویر اصلی است .

% % Wiener Deconvolution
NSPR1 = 0 ;
Fhat 1 = deconvwnr (g2 , PSF , NSPR1 ) ;
ImageVar = Var (f (:) ) ;
NSPR2 = NoiseVar / ImageVar ;
Fhat2 = deconvwnr (g2 , PSF , NSPR2 ) ;
NSPR3 = 0 .05 ;
Fhat3 = deconvwnr (g2 , PSF , NSPR3 ) ;
% % Results
figure ;
subplot ( 2 , 3 , 1 ) ;
imshow ( f ) ;
title ( ‘ Original Image ‘ ) ;
subplot ( 2 , 3 , 2 ) ;
imshow ( g1) ;
title ( ‘ Blurred Image ‘ ) ;
subplot ( 2 , 3 , 3) ;
imshow ( g2) ;
title ( ‘ Blurred and Noisey Image ‘ ) ;
subplot ( 2 , 3 , 4) ;
imshow ( fhat1 ) ;
title ( ‘ Recovered Image ( NPSR = 0 ) ‘ ) ;
subplot ( 2 , 3 , 5) ;
imshow ( fhat2 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR2) ‘ ) ‘  ] ) ;
subplot ( 2 , 3 , 6) ;
imshow ( fhat3 ) ;
title ( [ ‘ Recovered Image ( NPSR = ‘ num2str ( NSPR3) ‘ ) ‘  ] ) ;

روش آماری NSPR در متلب

نویز را بیشتر حذف کرده ولی حالت بلوری وتار شده اش بیشتراز قبلی است اما نسبت به تصاویر بالا شفافتر وبهتر است .

میخواهیم از روش دیگر J = deconvwnr ( I , PSF , NCORR , ICORR ) هم برای فرا خوانی استفاده کنیم .

اول طیف نویز را به دست میاوریم .

SN = abs (fft2 (g2 – g1)) . ^2 ;
NCORR = fftshift (real (ifft2 (SN)) ;
SF = abs (fft2(f)) . ^2 ;
FCORR = fftshift (real (ifft2 (SF))) ;
NSPR = NCORR . / FCORR ;
Fhat3 = deconvwnr ( g2 , PSF , NCORR , FCORR ) ;

روش تابع deconvwnr در متلب

کُریلیشن سیگنال با خودش است یعنی نسبت به مختلف عوض میشود لذا یک عدد ثابت نیست (با یک عدد ثابت با همه جای تصویر برخورد نمیکند)

یک جاهایی از تصویر خراب شده ولی خود تصویر دارای وضوح زیادی است بهتر از تصویر حاصل شده از آنالیزه کُریلیشن است برای حذف خطوط افقی عمودی روی تصویر ازتابع J = edgetaper (I , PSF) استفاده میکنیم که بخشی از کناره های تصویر رابه حالت خاصی محو میکند .

PSF2 = fspecial (‘gaussian ‘ , 60 , 10 ) ;
Fhat4 = edgetaper (fhat3 , PSF2 ) ;

تابع edgetaper در متلب

حاشیه ها را محوتر کرد .

میبینیم با هر کدام از فیلتر ها چقدر نتیجه متفاوت حاصل میشود .

حذف نویز واصلاح تصویر در متلب 3 (21)